算法图解-常用排序
冒泡排序
冒泡排序简单来说,就是从左到右排序,如果右边较大,交换二者位置,继续遍历直到末尾得到最大值。
冒泡排序图解如下: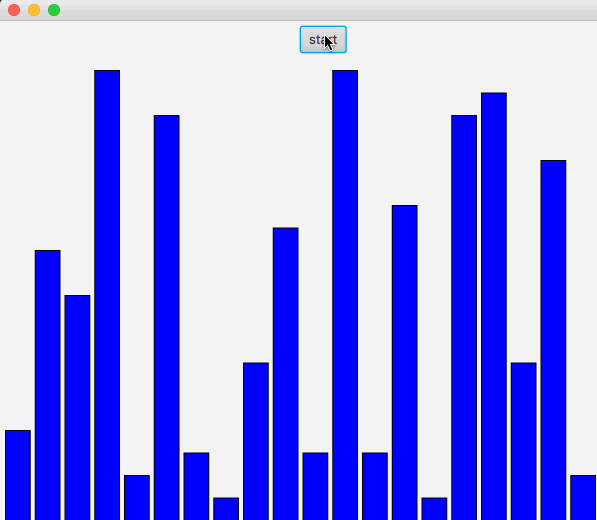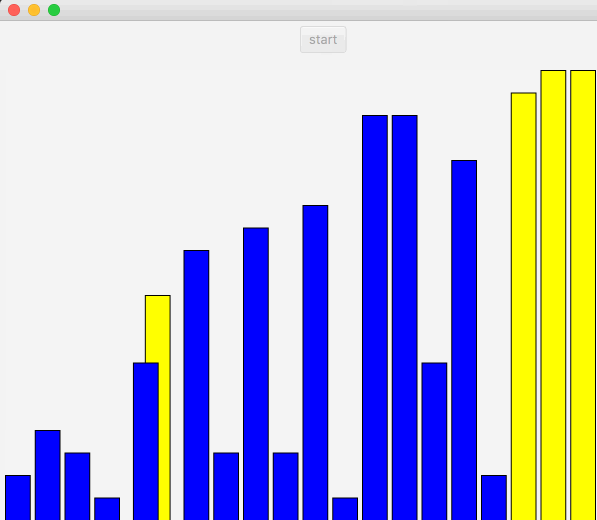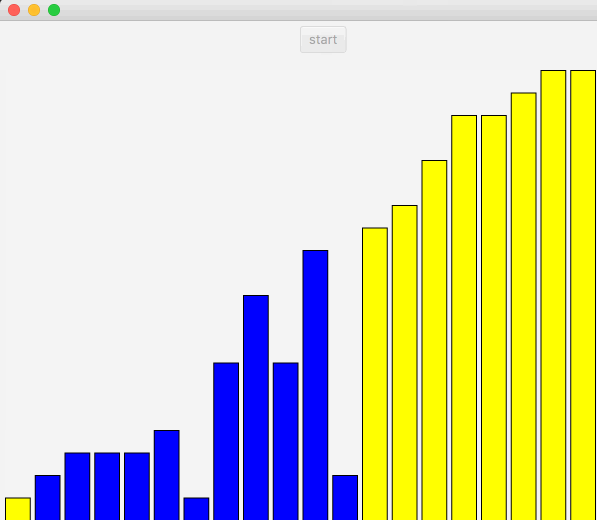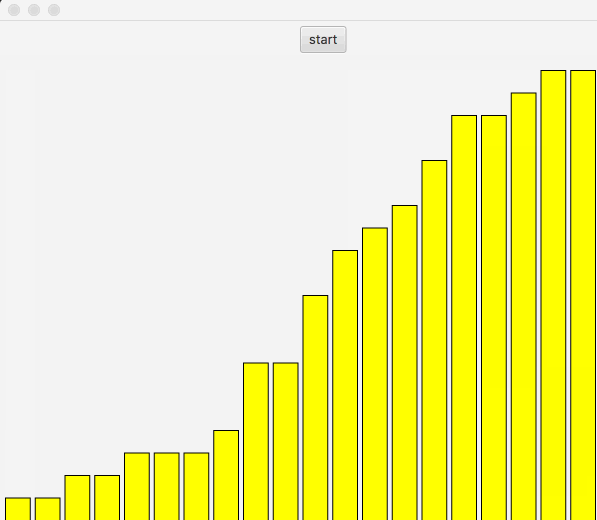
图中先从第一个开始,依次和右边比较,如果右边较大就进行替换,直到末尾。
代码如下:
1 | private int[] data; |
代码中包含了图形变换代码,直接忽略即可。
wikipedia·冒泡排序
选择排序
选择排序和冒泡类似,先找到最大或者最小值。放入数组首尾。
先看图: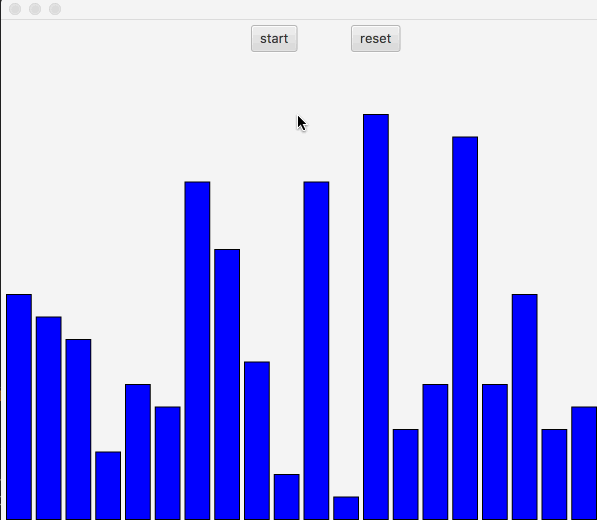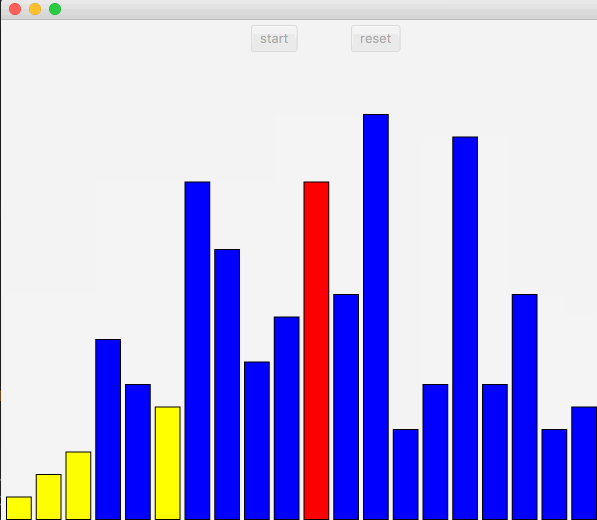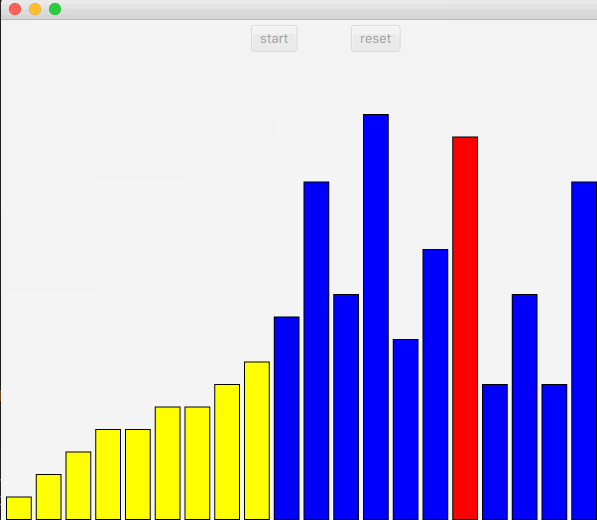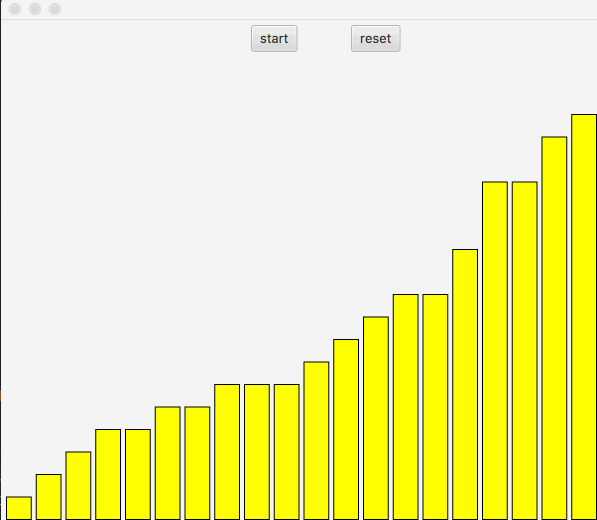
代码如下:
1 | public void sort() { |
向右遍历,记录最小索引,放入最左边,直到数组遍历完毕。
wikipedia·选择排序
插入排序
插入排序,在遍历过程中,保证左边已经是排好序,遍历的下一个数需要在已经排序的数组中找到自己的位置。
动图如下: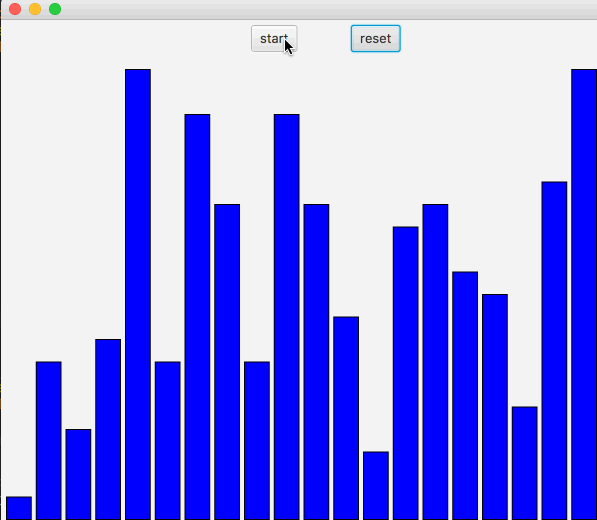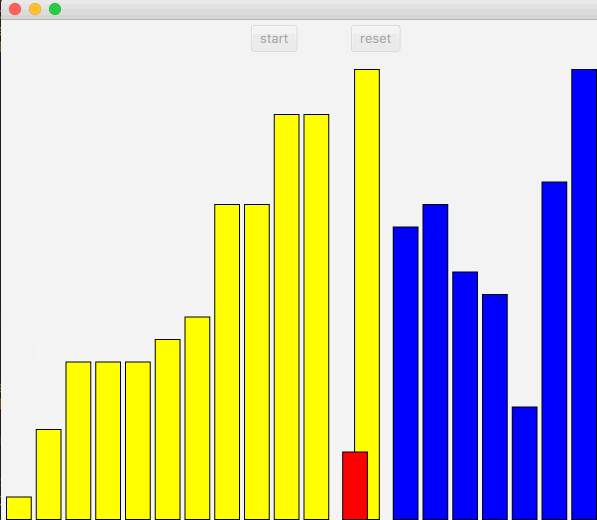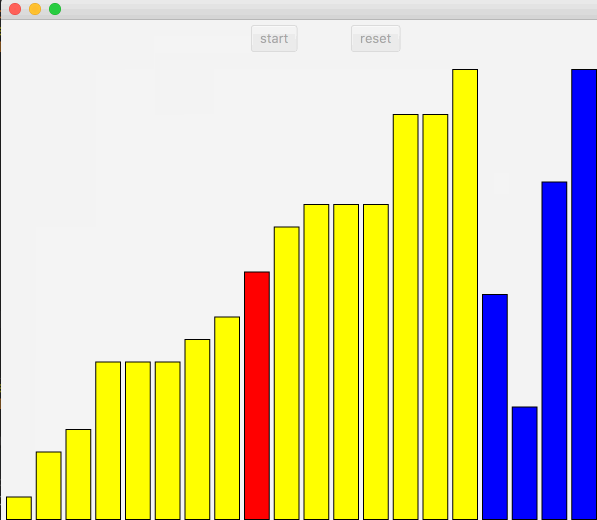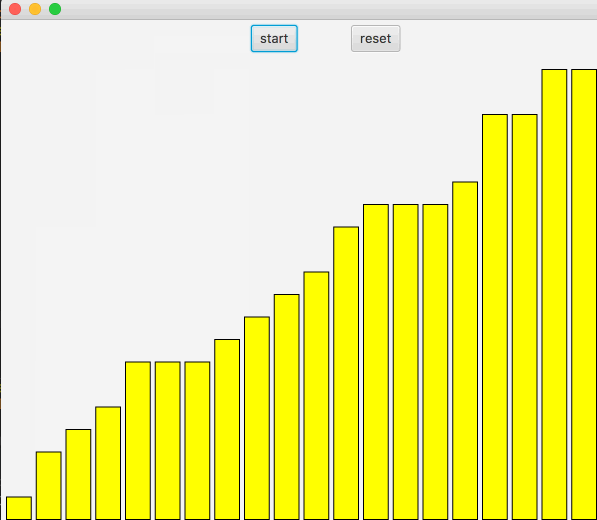
1 | public void sort() { |
上述代码中,先从左侧开始遍历,然后遍历中的节点开始向右比较,直到直到正确的位置。
wikipedia·插入排序
并归排序
并归排序是一种分治算法,把一个大数组先合并为一个个小数组,对小数组进行排序,之后再把小数组进行合并排序,直到最终合并为一个排好的大数组。在并归排序中需要引入额外的空间。
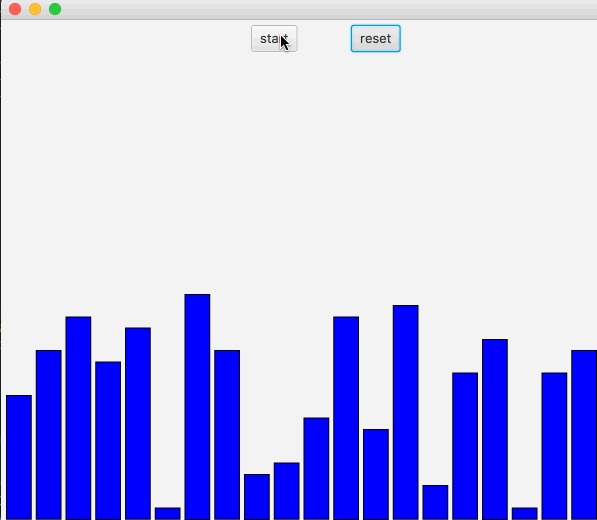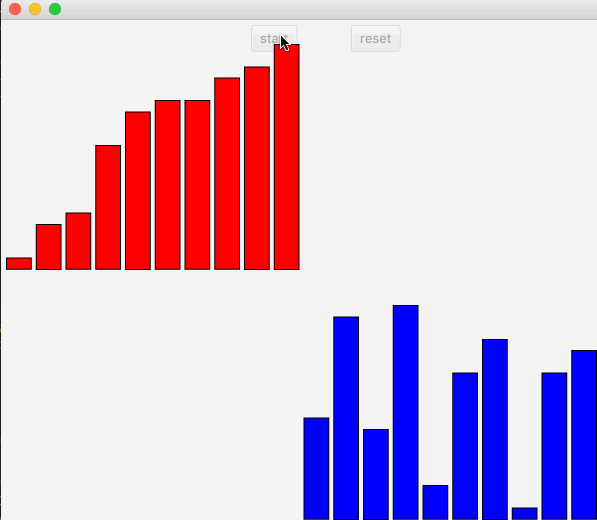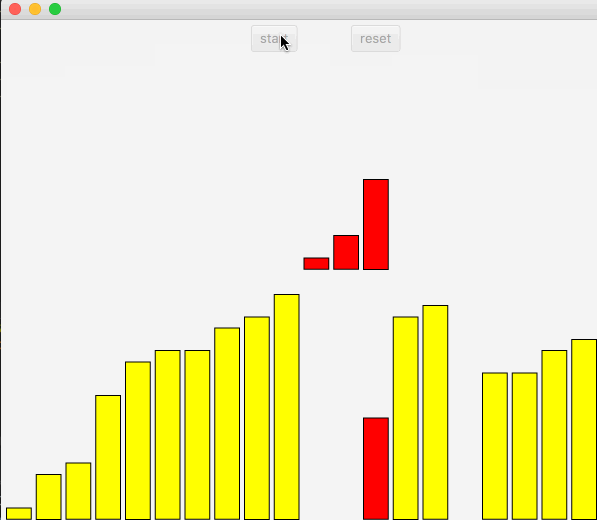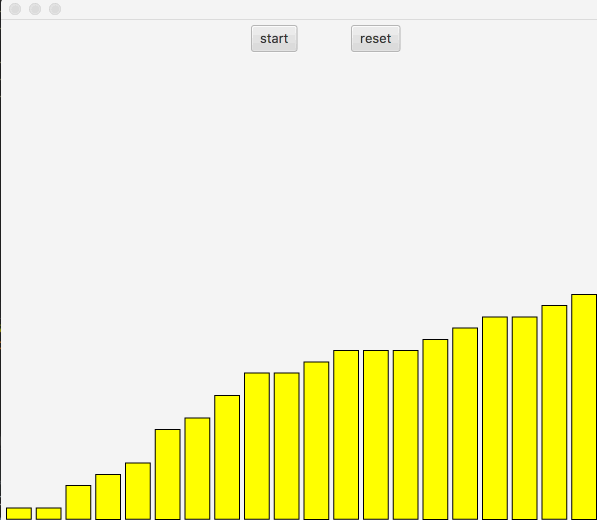
上述图中可以看出,先是把数组进行对半分,直到划分为最小数组长度1~2,然后小数组排序后,在合并大数组。对于并归排序中可以采用Java中Fork/Join进行加速排序
1 | public void sort() throws Exception { |
并归代码中无关代码较多。很多图形移动的逻辑。需要进行进一步封装。
上述代码中就是通过不断的拆分数组,然后对拆分的数组进行排序,只对排序的数组进一步排序直到结束。其中一部分逻辑就是从已经排序好的两个数组进行合并,也就简单的从两个数组中取值进行比较,直到某个数组值取值完毕,然后对移动另一个数组中的数剧到末尾。
wikipedia·归并排序
快速排序
快速排序基本原理是,先从数组中随机找一个基准,然后把小于改基准的值放入左边,大于改基准的值放入右边。然后对左右两边的数组进行递归同样的方法,找到随机值,小的放到左边,大的放到右边。
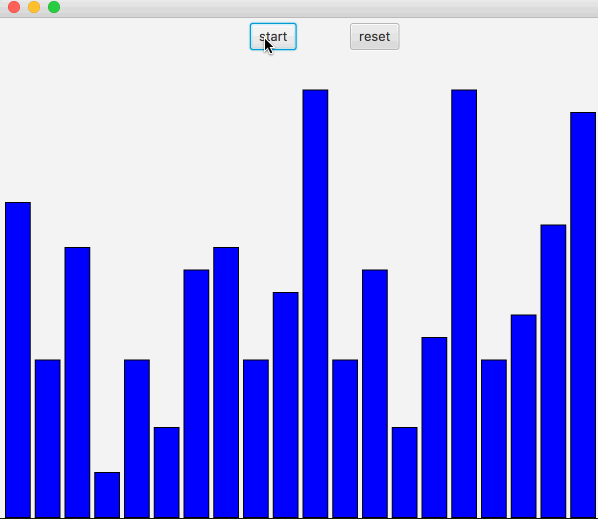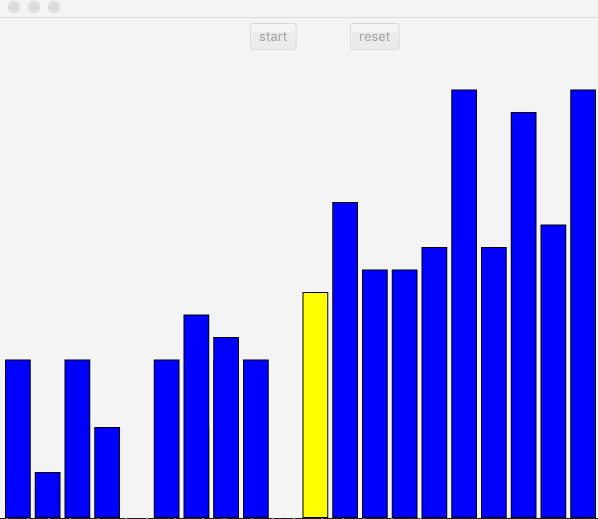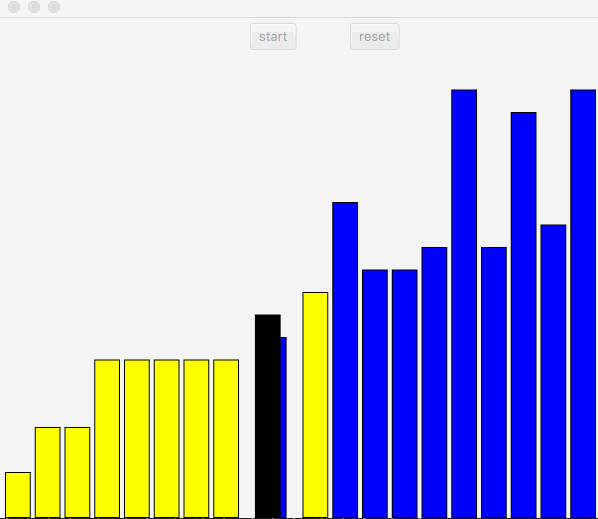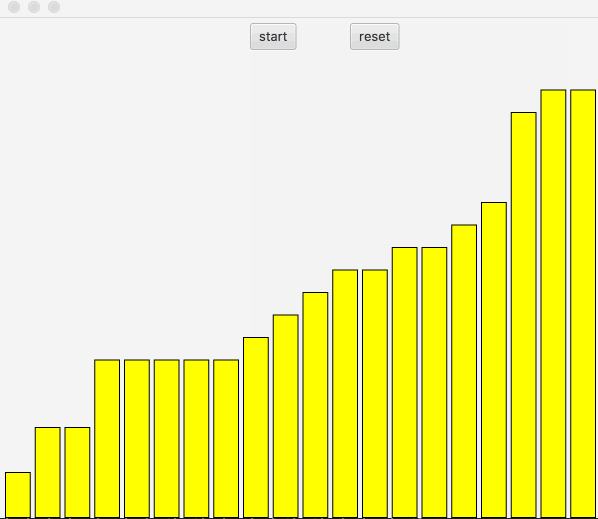
图中,黑色表示基准,先把获取的基准放入最右边,从左到右遍历,记录放入左侧的位置,如果遍历过程中值小于基准值,那么把该值替换到左侧记录的位置,位置左移,继续遍历,直到末尾,把基准插入左侧记录的位置。继续递归,直到结束。
1 | public void sort() throws Exception { |
wikipedia·快速排序
堆排序
堆排序的要点在于,先对数组构造一个完全二叉树,之后对二叉树取最高点,之后重新构造二叉树,重复上述步骤,直到取值完毕。
需要用的的知识点:
- 父节点i的左子节点在位置
(2i+1); - 父节点i的右子节点在位置
(2i+2); - 子节点i的父节点在位置
floor((i-1)/2);
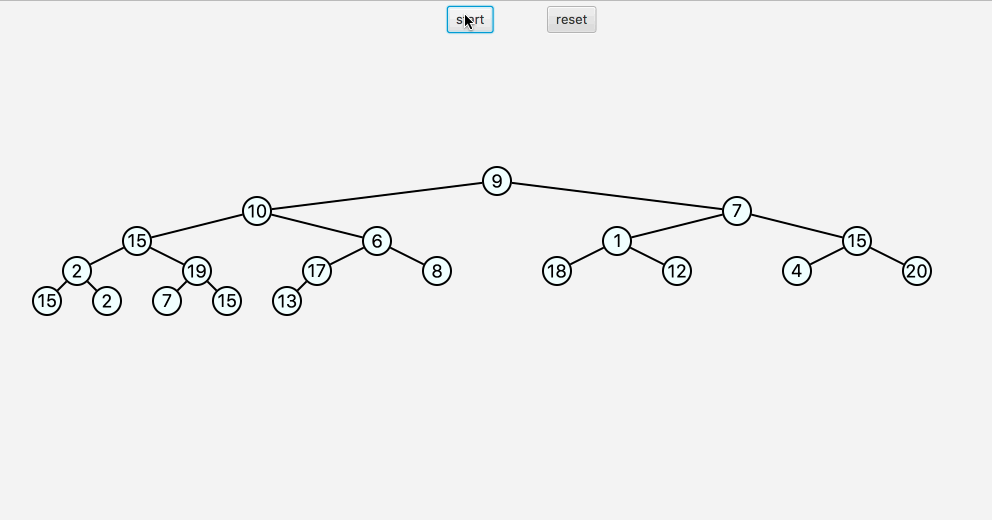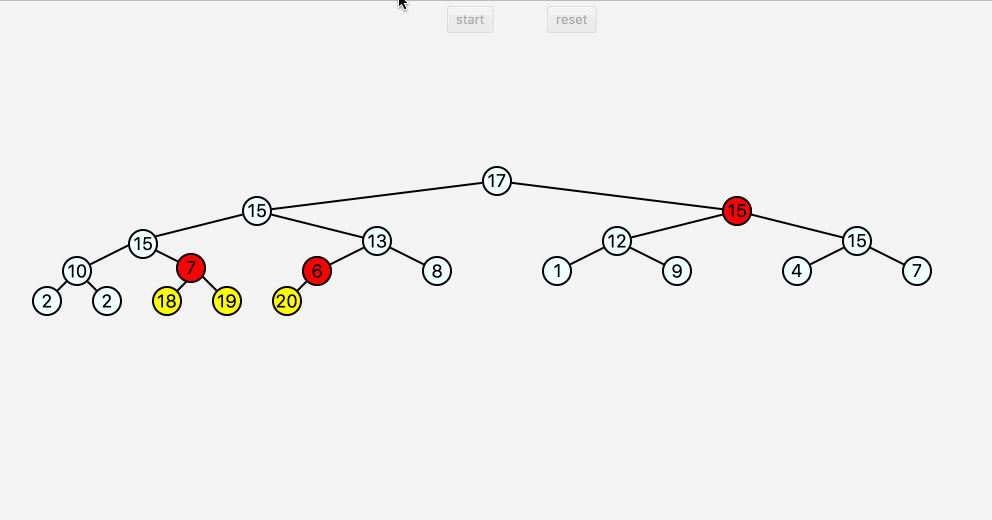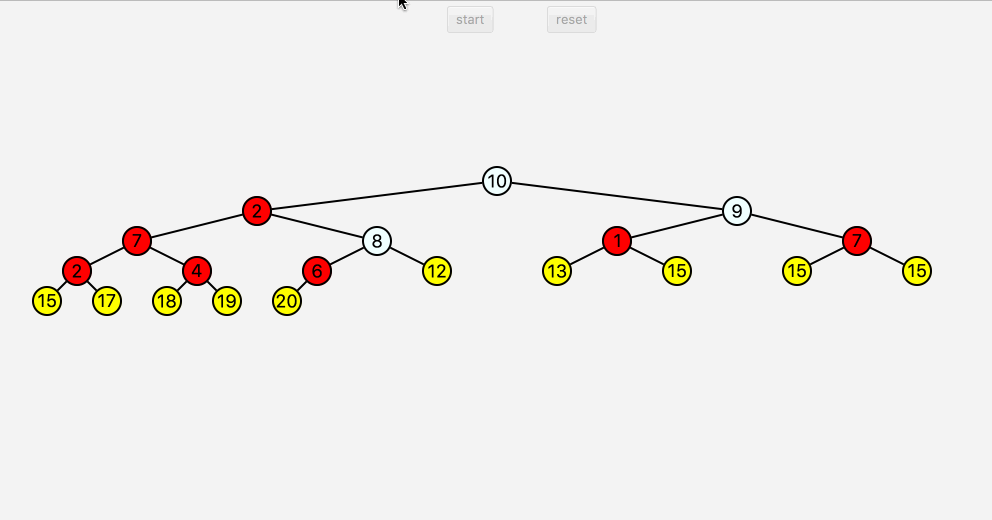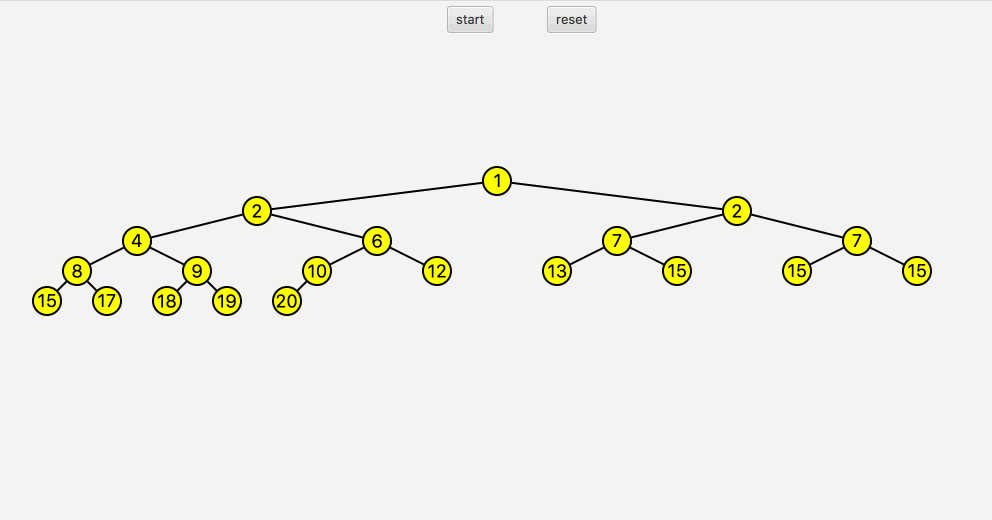
1 | //用于方便画图 |
附赠python3的排序
1 | def bubble_sort(nums): |
在上述图形化中,因为为了展现较好的效果,做了图形移动。如果不需要由移动效果,可以直接保存数组,在每次数组变动后,清除图形,然后依据变化后的数组重新画图,那么相对而言更为简单。
wikipedia·堆排序
各种排序复杂度: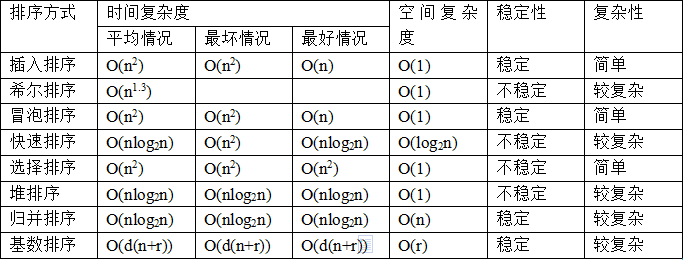
- 常用排序算法稳定性、时间复杂度分析
源码地址:https://github.com/whhxz/graphic-algorithm