算法-全排列

发表于 更新于 分类于

全排列：从包含n个不同元素的数组中，取m个数组，按照一定顺序排列不重复，当m=n时为全排列

如：现在数组[1, 2, 3]的全排列，[1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1]

实际数量有n!种可能。

递归

对于数组[1, 2, 3] 从0开始分别交换值得到数组：[2, 1, 3]、[3, 2, 1]，得到的3个数组（包含原数组）从1开始向后进行交换：[1, 2, 3] –> [1, 3, 2]、[2, 1, 3] –> [2, 3, 1]、[3, 2, 1] –> [3, 1, 2]

图形如下：

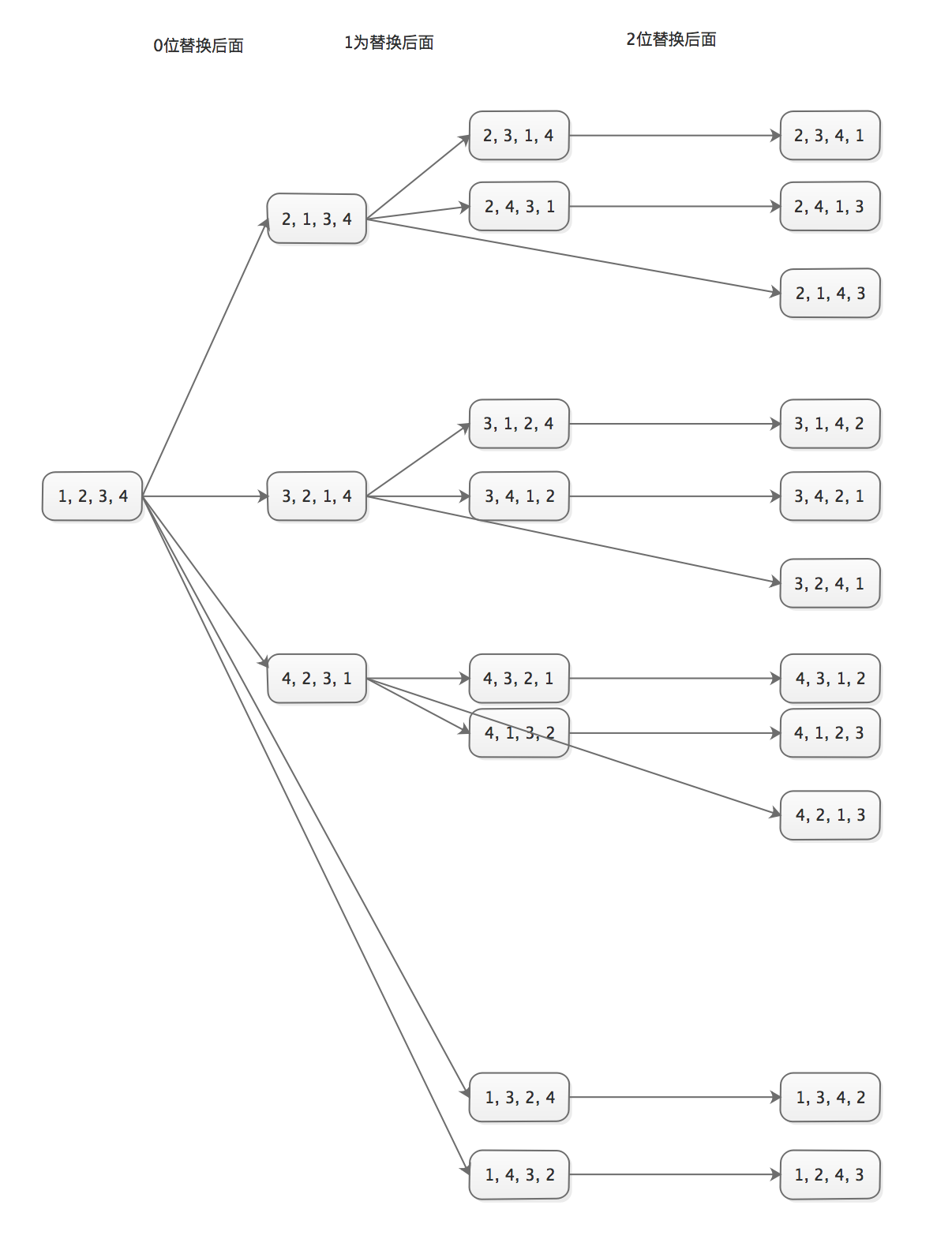
每次都是从上一个获取到的数组进行向后替换，可以提供递归完成，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        result_list = []
        self.array(nums, result_list, 0)
        return result_list

    def array(self, nums, result_list, start):
        # 递归到末尾结束
        if start == len(nums):
            return
        # 遍历从指定index向后遍历
        for i in range(start, len(nums)):
            swap_index = i
            # 交换数据
            nums[start], nums[swap_index] = nums[swap_index], nums[start]
            # 为了避免重复添加
            if start != 0 and i == start:
                pass
            else:
                # 添加数据进集合
                result_list.append(nums.copy())
            # 获取到的数组继续向后递归，起始从当前+1开始
            self.array(nums, result_list, start + 1)
            # 还原修改后的数组，用于下次遍历
            nums[swap_index], nums[start] = nums[start], nums[swap_index]

print(Solution().permute([1, 2, 3, 4]))

字典排序

itertools库中permutations

置换循环?
还要一种全排序，由python itertools库中permutations，简化版如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        # 通过原有nums生成len(num)~1倒排序
        cycles = list(range(len(nums), 0, -1))
        result_nums = [nums.copy()]
        while True:
            for i in reversed(range(len(nums))):
                cycles[i] -= 1
                if cycles[i] == 0:
                    nums[i:] = nums[i + 1:] + nums[i:i + 1]
                    cycles[i] = len(nums) - i
                else:
                    j = cycles[i]
                    nums[i], nums[-j] = nums[-j], nums[i]
                    result_nums.append(nums.copy())
                    break
            else:
                break
        return result_nums

没看明白